Actividad 2
Operaciones con fracciones: multiplicación y división
Vamos a ver ahora en qué situaciones se hacen necesarias las operaciones de multiplicación y división con fracciones.
¿Cómo se realizan estas operaciones? Algo sobre la multiplicación ya visteis en 5º. Vamos con ello.
Fuente imagen: http://www.mathematicsdictionary.com/spanish/ vmd/full/m/multiplicationoffractions.htm
Actividad
Vamos a analizar y resolver cada una de las siguientes situaciones. Elige a un compañero o compañera e intentad resolverlas en el cuaderno. Luego haz clic y en cada una de ellas elige la operación que deberás realizar para resolverla.
Resolveremos ahora cada una de las situaciones planteadas y veremos con ello cómo se realizan las actividades de multiplicación y división con fracciones. A ver si lo habéis hecho bien. Para ello, haz clic aquí: Operaciones con fracciones.
En vuestra vida diaria habréis observado que las proporciones entre las cosas (las fracciones que estamos trabajando) se expresan muy a menudo en porcentajes. No decimos “Edurne Pasabán ha
Por eso es tan importante que sepáis encontrar porcentajes a partir de una fracción. Para ello la regla es muy sencilla, veámosla con la fracción:
Utilizamos la calculadora y dividimos 5 : 48
Multiplicamos el resultado por 100 (corremos la coma dos lugares a la derecha) y obtenemos:
Por tanto 10,4 % es la solución.
Ahora añadid a las notas que habéis tomado en el cuaderno de la presentación anterior los porcentajes correspondientes:
Las calculadoras tienen una tecla que sirve para encontrar a qué cantidad corresponde un cierto porcentaje, es decir: “SI la montaña que escaló Edurne Pasabán era el Everest, que mide 8.848 m, y sabemos que la primera mañana escaló el 10,4%, ¿a qué altura llegó?
El proceso con la calculadora es:
Observa que usamos
Y ahora vosotros/as:
- Si tenemos un total de 250 paquetes de caramelos para repartir entre los alumno/as de Educación Infantil en la fiesta del colegio y sabemos que los porcentajes de alumnos son 30% los de 1º, 34% los de 2º y 36% los de 3º, ¿Cuántos paquetes debéis reservar para cada curso?
RECUERDA:
Para las operaciones entre números enteros y fracciones será importante tener en cuenta que:
|
a) Resolved las operaciones que encontraréis aquí: actividad_2_a.zip (.ods).
Solución: actividad_2_a_soluciones.zip (.ods).
b) En la siguiente actividad tendréis que elegir si hay que multiplicar o dividir en cada una de las operaciones: Seleccionar.
c) Ahora tendréis que completar las fracciones que faltan en cada una de las operaciones con fracciones: Calcular.
La calculadora. Uso con fracciones interesantes
Ahora que ya sabéis sumar, restar, multiplicar y dividir fracciones, vamos a plantearnos nuevos retos.
Es importante que utilicéis la calculadora (la vuestra o la que hay aquí) siempre que consideréis que os facilita los cálculos. Pero también es muy importante que intentéis hacer los cálculos mentalmente, sin usar bolígrafo ni calculadora (siempre que podáis).
Cojamos un número cualquiera, 246 y hagamos con él estas operaciones:
Efectivamente, en los tres casos os da 123. ¿Por qué?
Es importante ese “por qué” porque nos va a facilitar mucho el cálculo mental. Pensad que multiplicar 450.684 por 0,5 es un rollo, pero dividirlo por 2 es muy fácil y con un poco de entrenamiento lo podéis hacer “de cabeza”: 225.342.
- ¿Ocurrirá al revés? ¿Es lo mismo dividir por 0,5 que multiplicar por 2?
Comprobadlo con el número 234.564.
¿Ocurrirá lo mismo? Comprobadlo con el número 564.
- ¿Sabrías encontrar una norma de cuándo y con qué números ocurre eso? Os facilitaría mucho los cálculos.
- Y una pregunta difícil: ¿ocurre lo mismo con el 3? ¿qué dificultades encuentras?
RECUERDA:
|
Las fracciones que son menores de la unidad (fracciones propias) son muy importantes, muchas veces oímos frases así:
- “Sólo se llenaron los tres cuartos del estadio”.
- “Después de tanto trabajo no he llegado ni a la mitad del que tenía que hacer”.
- “Hemos acabado el primer trimestre del curso pero todavía nos quedan dos tercios”.
Estas fracciones forman parte continua de nuestra vida y debes dominarlas. Unas cuantas preguntas sobre ellas, intentad responderlas “de cabeza” y si no, utilizad la calculadora:
- Si he hecho la mitad de mi trabajo ayer y otro tercio hoy, ¿he terminado el trabajo?
- Si tengo una botella de un litro, echo en ella primero un tercio de litro y después tres cuartos, ¿la llenaré?, ¿desbordará el líquido?
- Si os dicen a vuestro grupo que debéis plantar en el jardín de vuestro centro, la mitad del espacio de rosas blancas, un cuarto de rosas rojas y un tercio de gladiolos, ¿cómo lo haréis?
Y la última: es importante que sepamos comparar entre si todas estas fracciones que tanto usamos en nuestra vida.
Ordena de menor a mayor las siguientes fracciones. Utiliza la calculadora cuando tengas dudas: divide y compara:
Haced clic en la imagen para utilizar la calculadora:
Y si tenéis dudas consultad este manual.
Titulo Multiplicación y división de fracciones
Descripción: Para repasar de forma gráfica las operaciones con fraciones.
Ayuda
- Menú izquierdo (en orden de arriba a abajo): icono página principal de la secuencia (home), icono tamaño de la fuente, icono impresión, icono acceso a la ayuda e icono índice del contenido.
- Barra nombre del material y título de la sección actual.
- Flechas de navegación (página siguiente o anterior).
- Espacio para el contenido.
Autor:
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Copyright:
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
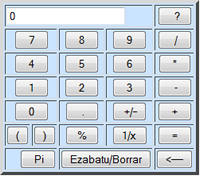
Tecla %
Operaciones con fracciones
Haz clic en la imagen para avanzar:
Soluciones
Soluciones
Soluciones
75 para 1º, 85 para 2º y 90 para 3º.
Soluciones
Eso ocurrirá con aquellos números que son inversos.
| [El inverso de 8 es |
|
y también 0,125 (1 : 8 = 0,125)] |
Los casos más sencillos son: el 0,5 y el 2, el 0,25 y el 4, pero pueden ser interesantes las unidades seguidas de ceros:
- 10, 1/10, 0,1
- 100, 1/100, 0,01
- 1.000, 1/1.000, 0,001
Soluciones
Las tres preguntas tienen en común el que necesitamos saber si la suma de las fracciones dadas en cada caso es mayor, menor o igual que 1:
No he terminado mi trabajo, me falta
Una forma más fácil: 1: 2 = 0,5, 1 : 3 = 0,33.., 0,5 + 0,33 = 0,83 < 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------
También: 1 : 3 = 0,33, 3 : 4 = 0,75, 0,33 + 0,75 = 1,08 > 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------
El trabajo es imposible, superamos el jardín
1 : 2 = 0,5, 1/3 = 0,33, 1 : 4 = 0,25, 0,5 + 0,33+ 0,25 = 1,08 > 1
Soluciones
Índice
- Operaciones con fracciones
- Guía para el profesorado
Créditos
DIRECCIÓN: Narcís Vives
COLABORADORES:
- PRODUCCIÓN EJECUTIVA: Antonio Cara
- DIRECCIÓN CONTENIDOS: Mª Cristina Pérez y Magdalena Garzón
- DIRECCIÓN TÉCNICA: Maite Vílchez
- COORDINACIÓN ÁREA MATEMÁTICAS: José Orenga
- AUTORÍA: Mª Rosa Urain
- CORRECCIÓN ESTILO VERSIÓN CASTELLANA: Anna Betriu y Joan Martín
- ADAPTACIÓN EUSKERA: Bakun itzulpen eta argitalpen zerbitzuak, s.l.
- MAQUETACIÓN: Maite Vílchez y Miquel Gordillo