MATEMATIKA-arloa
Irakasleentzako gida
AurkezpenaOrientabideakOrientabideakOrientabideakOrientabideakProgramazioaProgramazioaProgramazioaProgramazioaOinarriakOinarriakOinarriakOinarriakOinarriakOinarriak
1 de 15
0%
Aurkibidea
Kredituak
Kredituak
© Itinerarium 2011 ZUZENDARITZA: Narcís Vives KOLABORATZAILEAK: PRODUKZIO-ZUZENDARITZA: Antonio Cara EDUKI-ZUZENDARITZA: Mª Cristina Pérez eta Magdalena Garzón MATEMATIKA ARLOAREN KOORDINAZIOA: José Orenga ZUZENDARITZA TEKNIKOA: Maite Vílchez EGILEA: Marcel David Pochulu eta Mª Cristina Pérez GAZTELERAZKO BERTSIOAREN ESTILO-ZUZENKETA: Anna Betriu eta Joan Martín EUSKARARA ITZULPENA: Bakun itzulpen eta argitalpen zerbitzuak, s.l. MAKETAZIOA: Maite Vílchez eta Miquel Gordillo

Aurkezpena

PROPOSAMENA TESTUINGURUAN KOKATZEA

Hasiera batean, zatiketen elementuei eta zatiketa motei (osoak eta zehatzak) buruzko informazioa bilatu beharko dute ikasleek Interneten. Informazio hori lehenengo jarduerak ebazteko erabiliko dute, eta, aurrerago, kontzeptu horiek erlazionatzeko gai izan beharko dute. Informazio-bilaketan, lehenengo kontzeptu horiek bildu eta txostenean adieraziko dira.

Ondoren, hiru zifrako edo gehiagoko zatiketa zatitzailedunak eta 10ez, 100ez, 1.000z... zatitzekoak egin beharko dituzte. Zatiketak egin beharreko problemak ebatz ditzaten ere eskatuko zaie, eta gaiari buruz dituzten ezagutzak erakutsi ahal izango dituzte horrela. Egokia irudituz gero, kalkuluak behar bezala egin dituzten aztertu ahal izango dute, "Eskuinaldean nabarmendutakoak" atalean ageri diren "bederatziaren proba" eta "hamaikaren proba" izenekoen bidez.

Azkenik, zenbait jarduera proposatuko zaizkie ikasleei, zatiketa baten elementuen arteko erlazioak finkatzeko; hau da, eragiketa horren algoritmoaren esanahia uler dezaten. Kalkulagailua pentsatuz erabilita, ikasitako kontzeptuak sendotuko dituzte, bai eta buruzko kalkulurako abilezia hobetu ere.

JARDUEREN SEGIDA

A etapa. Sarrera: 1. jarduera. Ikasleek zatiketetan ageri diren elementuak eta zatiketa motak bereizten ikasiko dute.

B etapa. Garapena: 2. jarduera.
Zenbait motatako zatiketak proposatuko zaizkie, arauak eta zatiketaren algoritmoaren oinarrizko prozedurak bereganatu ditzaten.

C etapa . Itxiera eta ebaluazioa: 3. jarduera.

Ikasleek zatiketa zailagoak egingo dituzte eta erabiltzen dituzten prozeduren gaineko arrazoiketak egingo dituzte.
  • Arloa: Matematika
  • Gaia: Zenbaki arrunten arteko zatiketa (hiru zifrako zatitzailea)
  • Unitate didaktikoa: Zenbakiak eta eragiketak
  • Maila: Lehen Hezkuntzako 5.a
  • Saio kopurua: 3

Ibilbidea

Gida honek atal hauek ditu:

Orientabideak

Orientabide metodologikoak

1. jarduera: Problema ebazteko informazioa bilatzen (saio bat)

Jardueraren helburua da ikasleek zatiketetan ageri diren elementuak edo gaiak (zatikizuna, zatitzailea, zatidura eta hondarra) identifikatzea, eta zatiketa zehatzak (hondarra zero dutenak) zatiketa osoetatik edo ez-zehatzetatik (hondarra zero ez dutenak) bereizten jakitea. Ez da zatiketak egiteko trebezia landu nahi, zatiketen gaiak eta zatiketa motak ezagutzea baizik. Zatiketaren algoritmoa lantzen ere hasiko dira, emaitzak egiaztatzeko eta erantzunak justifikatzeko.


2. jarduera. Zatitu dezagun! (saio bat)

Jardueraren helburua da ikasleek hiru zifra arteko zatiketa zatitzailedunak ebazten eta egiaztatzen trebetasuna eskuratzea, eta zatitzailea 10, 100, 1.000... duten zatiketak egiteko arau bat ondorioztatzea. Irakasleari egokia irudituz gero, "Baliabideak" izeneko atalean ageri diren "bederatziaren eta hamaikaren probak" izenekoak azaldu (edo aztertu) daitezke.


3. jarduera. Zatiketez gehiago ikasten (saio bat)

Jarduera honen bidez, ikasleak ohartuko dira 10ez, 100ez, 1.000z... biderkatuz zatiketa baten zatidurak zenbat zifra izango dituen jakin daitekeela, eta, horren ondorioz, zatidura iritzira kalkula daitekeela. Gainera, azalduko zaie, zatiketa baten emaitza lor daitekeela, zatikizun txikiagoak hartuta (emandako zatikizuna biderketa moduan jarrita).

Azkenik, zatiketen gaien arteko erlazioa finkatu nahi da: zatikizuna = zatidura x zatitzailea + hondarra (hondarra zero edo handiagoa eta zatitzailea baino txikiagoa izanik). Horrez gain, bultzatu nahi da kalkulagailuaren erabilera kritikoa.

Orientabideak

Erantzunak

1. jarduera: Problema ebazteko informazioa bilatzen (saio bat)

Lehenengo jardueraren erantzuna hau edo antzekoren bat izan daiteke:

Zatiketaren elementuak edo gaiak: definizioa

Zatikizuna zatituko den zenbakia da.

134

Zatitzailea zatikizuna zatitzen duen zenbakia da.

15

Zatidura zatiketaren emaitza da.

8

Hondarra zatikizunean sobera geratu dena da, zatitzailea baino txikiagoa delako zatitu ezin izan dena.

14

Bigarren jardueran, horrelako erantzunen bat espero da:

Zatiketak: hondarraren araberako sailkapena

Zatikizuna zatitzailea bider zatidura baldin bada, ez dago hondarrik (hondarra zero da) eta zatiketa zehatza dela esaten da.

Zatikizuna zehazki zatitzailea bider zatidura ez bada, hondarra geratzen da (hondarra ez da zero), ez da zatiketa zehatza, eta zatiketa osoa edo ez-zehatza esaten zaio.

Erantzun posibleak:

  • “ Zatiketa bat zehatza da hondarra zero bada, eta osoa edo ez-zehatza, hondarra zero ez bada. ”.

  • Erantzuna hau izango litzateke:

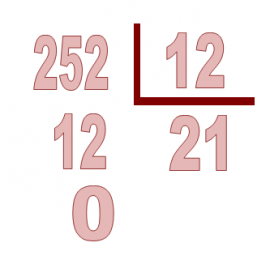
28:4 ZEHATZA

45:5 ZEHATZA

37:7 EZ-ZEHATZA EDO OSOA

73:8 EZ-ZEHATZA EDO OSOA

45:9 ZEHATZA

27:3 ZEHATZA

  • Zatikizunari Zk, zatitzaileari Zt, zatidurari Zd eta hondarrari H esaten badiegu, erantzuna hau da:

28:4

Zk. 28, Zt. 4, Zd. 7, H. 0

45:5

Zk. 45, Zt. 5, Zd. 9, H. 0

37:7

Zk. 37, Zt. 7, Zd. 5, H. 2

73:8

Zk. 73, Zt. 8, Zd. 9, H. 1

45:9

Zk. 45, Zt. 9, Zd. 5, H. 0

27:3

Zk. 27, Zt. 3, Zd. 9, H. 0

  • Jardueraren erantzuna irekia bada ere, esan beharra dago helburua dela ikasleak zatiketaren gaiekin eta zatiketaren hondarren araberako sailkapenarekin ohitzea. Gainera, aldi berean, zenbaki arrunten arteko zatiketaren algoritmoa lehen aldiz ikusiko dute.

  • Parte-hartzaileak 625 badira eta autobus bakoitzak 45 pertsona eramaten baditu, 45ez biderkatzean 625 ematen duen zenbakirik badagoen aztertu beharko litzateke. Horretarako, 625:45 zatiketa egin, eta zatidura 13 eta hondarra 40 direla ikusten da. Hau da, 625 = 13 x 45 + 40 erlazioa lortzen da. Emaitza horrek adierazten du pertsona guztiak ezin izango direla eraman, eta 40 lagun bidaiatu gabe geratuko direla (585 bakarrik eraman ahal izango dira); autobusak beterik egon ezean, ez baitira ateratzen. Parte-hartzaileen kopuru hori (585) eramateko 13 autobus beharko dira. Guztiak (625) eraman nahi badira, beste autobus bat beharko da, eta 5 pertsona gehiago beharko dira autobusa betetzeko.

2. jarduera. Zatitu dezagun! (saio bat)

1.2 ariketaren erantzuna honelakoren bat izango da: “Zenbaki bat 10ez, 100ez, 1.000z... zatitzeko, koma eskuinetik ezkerrera mugitu behar da, zeroen kopurua adierazten duen zenbakia adina posizio”.

2.3 ariketaren erantzuna:

Eragiketa

Emaitza

Eragiketa

Emaitza

543 : 1.000 =

0,543

7 : 100 =

0,07

134 : 100.000 =

0,00134

8 : 10.000 =

0,0008

300 : 100.000 =

0,003

3 : 10 =

0,3

26 : 100 =

0,26

60 : 1.000 =

0,06

25 : 10.000 =

0,0025

15 : 1.000 =

0,015

45 : 100 =

0,45

340 : 10 =

34

36 : 10.000 =

0,0036

20 : 100 =

0,2

805 : 10 =

80,5

18 : 100.000 =

0,00018

69 : 10.000 =

0,0069

689 : 1.000 =

0,689

22 : 100.000 =

0,00022

256 : 10 =

25,6

2. ariketaren erantzuna irekia dela esan daiteke, aipatutako web-orriko aplikazioak ausaz proposatzen dituen eragiketen araberakoa baita. Ikusi ebaluazio-irizpideak.

3. jarduerari dagokionez, ikasleek, planteatutako zatiketak ondo ebatzi ondoren, matematikari alemanaren izena zein den jakitea espero da.

Jardueraren erantzuna dokumentu honetan ikus daiteke.

Orientabideak

Erantzunak

3. jarduera. Zatiketez gehiago ikasten (saio bat)

Jarduera honen zailtasunik handiena da zatitzaileak zenbait eredutan bi gauza adierazten dituela ulertzea. Batetik, hasierako kantitatea zenbat zatitan banatzen den adieraz dezake; eta, bestetik, guztia banatzean osatzen diren zatiak lortzeko balio duen kopuru finkoa. Hori dela eta, irakaslearen laguntza beharrezkoa da etapa honetan.

Jardueraren erantzuna irekia dela esan badaiteke ere, hau erantzun behar lukete irakaslearen laguntzaz:

1. jarduera:

Ebatzi jarduera hauek, eta gorde erantzunak eta horien justifikazioak testu-prozesadorean.

  • Ikaskide batekin batera, proposatu zatitzailea 45 eta hondarra 12 dituen zatiketa bat.

Zenbaki bat aurkitu behar da (zatikizuna), eragiketa honen emaitza dena: beste zenbaki bat (zatidura) bider 45 eta gehi 12. Hau da, erlazio hau bete behar da: zatikizuna = 45 x zatidura + 12. Beraz, 45 (zatitzailea) edozein zenbaki arruntez (zatidura) biderkatu eta 12 (hondarra) batzea nahikoa izango da. Hona hemen zenbait adibide:

57 = 45 x 1 + 12

102 = 45 x 2 + 12

147 = 45 x 3 + 12

192 = 45 x 4 + 12

…

  • Begiratu aurreko atalean eman duzuen erantzuna, eta erantzun galdera hauei: Zatiketa bakarra al dago? Zenbat daude? Zergatik?

Zatitzailea 45 eta hondarra 12 duten infinitu zatiketa daude. Aurreko adibideetan ikus daitekeen eta lehen aipatu den erlazioa bete behar da, ez besterik.

  • Aurreko bi atalak oinarri hartuta, erantzun: Egia al da lortuko ditugun zatikizun guztien azkenengo zifra 7 edo 2 izango dela? Zergatik?

Aurreko itemetan landutakoaren arabera, zatikizun guztien azkenengo zifra 7 edo 2 dela ikus daiteke:

    • Zatidura zenbaki arrunt bat da; beraz, bikoitia edo bakoitia izan daiteke.

    • 45 zenbaki bikoiti batez biderkatzean, emaitzaren azkenengo zifra 0 izango da. 12 batzean, zatikizunaren azkenengo zifra 2 izango da.

    • 45 zenbaki bakoiti batez biderkatzean, emaitzaren azkenengo zifra 5 izango da. 12 batzean, zatikizunaren azkenengo zifra 7 izango da.

Erreparatu aurreko hiru galderei: Aurkitu al duzue 1.000 baino handiagoa den zatikizun bat eta horri dagokion zatidura? 1.000 baino handiagoak diren zatikizun horietatik zein da txikiena? Zatiketa batean zatikizuna 45 eta zatidura 11 badira, zein da zatitzailea? Eta hondarra?

Ikasleek zatiketaren gaien arteko erlazioa interpretatzea lortu badute, zatitzailea 45 eta hondarra 12 badira, eta horrek zatikizunean nola eragiten duen ulertu badute (azkenengo zifra beti 2 edo 7 izango da), ez dute zailtasun handirik izango 1.000 baino handiagoa den eta aurreko baldintzak betetzen dituen zatikizuna aurkitzeko. Gainera, seguruenik bururatuko zaien lehenengoa 1.002 izango da. Hala ere, 1.000 baino handiagoa den eta azkenengo zifra 7 duen hurrengo zenbakiak (1.007) ez du erlazioa betetzen. Azpimarratu behar da beharrezkoa dela zatikizunaren azken zifra 2 edo 7 izatea, baina ez dela baldintza nahikoa; hau da, erlazio hau bete behar du: zatikizuna = 45 x zatidura + 12. Hots, 1.002ren ondoren dagoen hurrengo gaia 45 bateko handiagoa izango da (zatitzailea eta hondarra finkatuta daudenez, zatidura handitu beharko dugu, eta zatidura bateko bat handitzean zatikizuna 45 bateko handituko da). Beraz, lehenengo galderaren erantzuna baiezkoa da. Bigarren galderaren erantzuna: 1.002.

Egokia irudituz gero, azaldu daiteke ezinezkoa dela zatikizunik handiena kalkulatzea (infinitu baitaude), murrizketaren bat kontuan hartu ezean (adibidez, 2.000 baino txikiagoa izatea). Hona hemen zenbait adibide:

1.002 = 45 x 22 + 12

1.047 = 45 x 23 + 12

…

1.992 = 45 x 44 + 12

  • Zatiketa batean zatikizuna 45 eta zatidura 11 badira, zein da zatitzailea? Eta hondarra?

Zenbakiak nahiko txikiak direnez (2 zifra), erraz ikusten da 11 zenbakia 45 zenbakian 4 aldiz "sartzen" dela. Horregatik, 45 beste zenbaki batez zatitzean 11 lortu nahi badugu, zenbaki horrek (zatitzaileak) 4 izan behar du. Zatitzailea 4 bada, hondarra 1 izango da, eta erlazio hau beteko da: 45 = 11 x 4 + 1.

Ikasleek ez baldin badute erantzuna erraz lortzen, zenbaki txikiagoekin has gaitezke; zatikizuna eta zatidura jakinik zatitzailea eta hondarra kalkulatzeko modua (zatitzailea kalkulatzeko, zatikizuna zatiduraz zatituz) ondorioztatzen lagunduko dieten zenbakiekin, hain zuzen ere. Zenbait adibide:

    • Zatikizuna 24 eta zatidura 4 badira, 24 “Zt” zenbakiaz zatitu beharko dugu 4 lortzeko. Hau da, “Zt” zenbakia kalkulatu behar dugu, 4z biderkatuz 24 emango duena, edo erlazio hau betetzen duena: 24 = 4 x Zt (Zatikizuna = Zatidura x Zatitzailea). “Zt” zenbaki hori 6 da eta 24 : 4 eginez lortzen da. Kasu horretan, zatiketaren hondarra zero da (zatiketa zehatza) eta erlazio hau betetzen da: Zatikizuna = Zatidura x Zatitzailea.

    • Zatikizuna 25 eta zatidura 7 badira, 25 “Zt” zenbakiaz zatitu beharko dugu 7 lortzeko. Hau da, “Zt” zenbaki arrunta kalkulatu behar dugu, 7z biderkatuz 25 emango duena. Hori ezinezkoa denez, zatiketa osoa edo ez-zehatza izango da, eta hondarra zeroren desberdina izango da. Beraz, erlazio hau betetzen duen “Zt” zenbakia aurkitu behar dugu: 25 = 7 x Zt + H (Zatikizuna = Zatidura x Zatitzailea + Hondarra). “Zt” zenbaki hori 3 da eta 25 : 7 eginez lortzen da, eta hondarra 4 da. Erlazio hau betetzen da: Zatikizuna = Zatidura x Zatitzailea + Hondarra; gure adibidean, 25 = 7 x 3 + 4.

  • Zatiketa batean zatikizuna 45 eta hondarra 1 badira, zein da zatitzailea? Eta hondarra? Zuen erantzunak berrikus itzazue eta pentsa ezazue ea beste erantzun posibleren bat dagoen. Baiezkoa bada, idatz itzazue aurkitu dituzuen guztiak.

Aurreko azterketan oinarrituz, ikasleak ohartu behar du bi zenbaki arrunt aurkitu behar dituela, biak biderkatuz 44 ematen dutenak; izan ere, zatiketa osoa edo ez-zehatza da, hondarra 1 delako. Hau da, bi zenbaki aurkitu behar dira, “Zt” eta “Zd”, erlazio hau betetzen dutenak: 45 = Zd x Zt + 1.

Aurreko jarduera ebatzi baldin bada, ikasleek ez dute zenbaki horiek aurkitzeko zailtasun handirik izango. Zenbait adibide:

45 = 1 x 44 + 1 (1 eta 44 zatidura eta zatitzailea edo zatitzailea eta zatidura izan daitezke, hurrenez hurren)

45 = 2 x 22 + 1 (2 eta 22 zatidura eta zatitzailea edo zatitzailea eta zatidura izan daitezke, hurrenez hurren)

45 = 4 x 11 + 1 (4 eta 11 zatidura eta zatitzailea edo zatitzailea eta zatidura izan daitezke, hurrenez hurren)

  • Zatiketa batean, izan al daitezke zatikizuna 32, zatidura 12 eta hondarra 1? Zergatik?

Galdera horri erantzuteko, ikasleek hau pentsatu beharko lukete: zenbaki bat aurkitu behar dugu, 12z biderkatuz eta emaitzari 1 batuta 31 emango duena. Ez dago ezaugarri hori betetzen duen zenbaki arruntik; hots, ez dago erlazio hau betetzen duen “Zt” zenbakirik: 32 = 12 x Zt + 1. Beraz, zatiketa hori ezin dela egin adierazi beharko dute.

  • Ariketa horiek guztiak egin ondoren, lortuko al zenukete zatiketa baten gaiak (zatikizuna, zatitzailea, zatidura eta hondarra) erlazionatzen dituen formularik? Dakizuenez, zatiketa zehatz batean, zatitzailea zatiduraz biderkatzean zatikizuna lortzen da: zatiketa osoetan ba al dago antzeko formularik? Idatzi ondorio guztiak testu-fitxategi batean eta aztertu beste taldeekin batera.

Jardueraren amaieran, ikasleek zatiketaren algoritmoa (zatiketaren gaien arteko erlazioa) ulertzea eta zuzentasunez erabiltzea lortu nahi da: Zatikizuna = Zatidura x Zatitzailea + Hondarra.

2. jarduera:

Ebatzi jarduera hauek:

  • Jakinik:

12 x 10 = 120

12 x 100 = 1.200

12 x 1000 = 12.000

12 x 10.000 = 120.000

Erabaki:

  • 130 : 12 10 baino handiagoa, txikiagoa edo berdina den.

  • 1.000 : 12, 100 baino handiagoa, txikiagoa edo berdina den.

  • 11.719 : 12, 1.000 baino handiagoa, txikiagoa edo berdina den.

  • 162.985 : 12, 10.000 baino handiagoa, txikiagoa edo berdina den.

Idatzi erantzunak testu-prozesadorean, eta justifikatu.

Hasieran, zailtasunak badituzte kalkulu horiek egiteko, banaketaren testuingurura eraman daiteke, eta hau galdetu: 130 € zati berdinetan banatuz gero 24 pertsonaren artean, bakoitzak 10 € baino gehiago ala gutxiago jasoko luke? Bakoitzak 10 € jasoko balitu, zenbat diru banatuko litzateke? Beste itemekin modu berean jokatu daiteke.

Lortu beharreko erantzunak hauek dira:

130 : 12 zatiketaren emaitza 10 baino handiagoa da.

1000 : 12 zatiketaren emaitza 100 baino txikiagoa da.

11719 : 12 zatiketaren emaitza 1.000 baino txikiagoa da.

162985 : 12 zatiketaren emaitza 10.000 baino handiagoa da.

3. jarduera:

Ebatzi jarduera hauek, eta jaso erantzunak testu-prozesadorearen bidez.

  • Jonek kalkulagailuz 15 : 2 egitean 7,5 lortu zuen. Gero, 15 : 4 egin eta 3,75 lortu zuen. Azkenik, 15 : 8 egin eta 1,875 lortu zuen. Emaitza horietatik abiatuz, nola lortuko zenukete zatiketa bakoitzaren hondarra kalkulagailua erabiliz? Azaldu prozedura eta egiaztatu eragiketak, prozedurak balio duela segurtatzeko. Prozedura hori erabiliz, kalkulatu 5.425 : 16 zatiketaren hondarra, kalkulagailua erabiliz 339,0625 emaitza lortu dela jakinik.
    • 15 : 2 = 7,5

Lortutako emaitza ez da zenbaki arrunt bat, zenbaki hamartar bat baizik. Eta honela irakurtzen da: “7 bateko, 5 hamartar”. Zenbaki horrek, beraz, zatiketaren zatidura 7 dela adierazten du, eta zatitzailea baino txikiagoa den hondar bat dagoela “sobera”. Hain zuzen ere, emaitzako “5 hamartarrak” hondarraren balioa adierazten du. “5 hamartar” “5 zati 10” bezala interpreta daitekeenez, eta 5 zenbakia 10en erdia denez, hondarrak zatitzailearen erdia izan beharko du. Kasu honetan, zatitzailea 2 da eta erdia 1 da. Horrela, 15 : 2 zatiketa osoan, badakigu zatidura 7 eta hondarra 1 direla; hau da: 15 = 7 x 2 + 1 (gogoratu zatiketa oso baten gaien arteko erlazioa). Zergatik ageri da kalkulagailuan 7,5 emaitza? Kalkulagailuaren bisorean 7,5 baino ageri ez denez, esan nahi du zatiketa horren hondarra zero dela. Hau da: 15 = 7,5 x 2; edo bestela: 15 = (7 + 0,5) x 2 = 7 x 2 + 0,5 x 2 = 14 + 1. Beraz, zer egin behar dugu kalkulagailuan 1 hondarra lortzeko? Egin dezagun azterketa hau: 7,5 emaitzak zatiketa osoaren zatidura 7 dela adierazten du, eta zatitzailea 2 denez, badakigu: 15 = 7 x 2 + H; edo beste era batean adierazita: 15 – 7 x 2 = H. Beraz, 15 – 14 = H, hau da, H = 1. Hori da lortu nahi genuen balioa.

    • 15:4 = 3,75

Aurrekoaren antzeko arrazoiketa egiten badugu: 15 = 3,75 x 4. Hortaz, badakigu zatiketa osoan zatidura arrunta 3 dela, eta, horren ondorioz, 15 = 3 x 4 + H betetzen dela. H kalkulagailuaren bidez kalkulatzeko hau egingo genuke: 15 = (3 + 0,75) x 4 = 3 x 4 + 0,75 x 4 = 12 + 3. Horrek adierazten du: H = 3.

    • 15 : 8 = 1,875; 15 = 1,875 x 8; 15 = (1 + 0,875) x 8; 15 = 1 x 8 + 0,875 x 8; 15 = 8 + 7. H = 7.

    • 5.425 : 16 = 339,0625; 5.425 = 339,0625 x 16; 5425 = (339 + 0,625) x 16 = 339 x 16 + 0,0625 x 16 = 5.424 + 1. H = 1.

Orientabideak

Baliabideak

Testu-prozesadorea
Beste zenbait aplikazio
Web-erreferentzia gomendagarriak

Programazioa

OINARRIZKO GAITASUNAK

Norberaren autonomiarako eta ekimenerako gaitasuna

  • Planifikatzea, baliabideak kudeatzea eta emaitzak balioestea, problemak ebaztean edo egoera irekietan.

  • Norberaren gaitasunetan konfiantza izatea, egoera ezezagunei aurre egiteko.

Ikasten ikasteko gaitasuna

  • Gero eta zailtasun handiagoko egoerak ebaztea autonomiaz, jarraikitasunaz, eta kemenez, eta emaitzak sistematizatzea eta balioestea; eta haien berri ematea.

Hizkuntza-komunikaziorako gaitasuna

  • Matematikako lexikoa zehaztasunez erabiltzea.

  • Norberaren eta besteen arrazoiketak ulertzea eta kritikoki balioestea.

Gizarterako eta herritartasunerako gaitasuna

  • Talde-lanean aritzea; ikuspuntu guztiak onartzea.

ARLOAREN BERARIAZKO GAITASUNAK

  • Batuketa, kenketa, biderketa eta zatiketa eguneroko bizitzako egoeretan erabiltzea, zenbait prozedura erabiliz (idatzizko algoritmoak, kalkulagailuaren erabilera, buruzko kalkulua, iritzirako kalkulua).

  • Eguneroko bizitzako egoeretan oinarritutako problemak interpretatu eta ebaztea, eta jarraitutako prozesua eta lortutako emaitzak ordenan, argi eta arrazoituta azaltzea eta aurkeztea.

Programazioa

IKT GAITASUN OROKORRAK ETA IKASMAILAKOAK*

* Lehen Hezkuntzako 5. mailako ikasleentzako “Eskola 2.0” proposamenaren IKT gaitasunerako itemak, eranskin honetatik hartuak: IKT gaitasunen mapa .

Bizitza osorako ikaskuntza

B1. Komunikatzea eta lankidetzan aritzea

  • B1.1. Haien inguruarekiko gertuko arazo sinpleetarako irtenbideak identifikatu eta ebaluatzea, eta kontzeptuak argitzea ahalbidetzen duten lankidetzako IKT baliabideak erabiltzea

B2. Ingurune birtualetan moldatzea

  • B2.1. Ingurune birtual bat maneiatzen hastea eta ingurune horietako oinarrizko eragiketak ikasteko gai izatea

B3. Informazioa kudeatu, sortu eta balioestea

  • B3.5. Dagokion arloko oinarrizko prozedurak eta metodoak aplikatzea, heldu baten laguntzaz

B4. Sortzaileak izatea eta berritzea

  • B4.2. Sormenaz, ikerketaz eta berrikuntzaz baliatuz, beren produktuak (bideo-jokoak, aurkezpenak, gailuak) sortzea ahalbidetzen dieten IKT baliabideak erabiltzea, beren interesak betetzeko edo beste batzuek planteatutako arazoei irtenbidea emateko

B5. Mundu erreala ulertzea, arakatzea eta bertan moldatzea

  • B5.1 Batez ere irudiak eta soinuak erabiliz eta heldu baten laguntzaz, mundu errealeko gaiak arakatzea eta/edo benetako arazo txikiei heltzea ahalbidetzen duten IKT baliabideak erabiltzea

Trebetasun teknologikoa

T3. IKTak testu-informazioa prozesatzeko erabiltzea

  • T3.1. Testu-prozesaketako oinarrizko eragiketak egitea (kopiatu eta itsastea; formatua, lerrokatzea eta orrikatzea zehaztea; irudiak txertatzea; tipografia eta tamaina aldatzea; dokumentuak artxibatu eta inprimatzea)

Programazioa

IKASKETA-HELBURUAK

  • Zatiketaren gaiak identifikatzea.

  • Zatiketa osoak (edo ez-zehatzak) eta zehatzak bereiztea.

  • Zatiketaren gaien arteko erlazioak ezagutzea.

  • Hiru zifrarainoko zatiketa zatitzailedunak egitea eta egiaztatzea.

  • Zatiketa baten zatidura kalkulatzea.

  • Buruzko kalkulurako estrategiak aplikatzea.

  • Kalkulagailua zentzu kritikoz erabiltzea, zatiketei buruz jasotako ezagutzak aplikatzea eskatzen duten problemak ebazteko baliabide bat modura.

  • Problemak ebaztean sortzen diren zailtasunak bideratzeko edo gainditzeko azalpenak, esperientziak eta prozedurak hausnartu, arrazoitu, jarraitu eta partekatzeko beharra balioestea, akatsak egitea barne.

  • Lan-taldean modu aktibo eta arduratsuan parte hartzea, eta ikasitako edukiak erabili beharreko problemak ebaztean ekimena izatea.

  • Norberaren ahalmenean eta autonomian konfiantza hartzea, akatsak, erronkak eta zenbait edukiri buruzko matematika-lanak gainditzeko.

  • Berariazko lexikoa zehaztasunez erabiltzea.

  • Baliabide informatikoak trebetasunez erabiltzea.

  • Problemak ebazteko metodoa aplikatzea.

EDUKIAK

  • Zatiketaren gaiak

  • Zatiketak egiaztatzea

  • Zatiketa osoak eta zehatzak

  • Hiru zifrarainoko zatiketa zatitzailedunak

  • Zatidurak iritzira kalkulatzea

Programazioa

EBALUAZIO-IRIZPIDEAK

  • Testu bat irakurri eta ulertzen du.
  • Problemak ebazteko, zenbakiak eta buruzko kalkulua zuzentasunez erabiltzen ditu.
  • Ondorio koherenteak eta lotuak lortzen ditu.
  • Lankidetzan aritzen da.

Oinarriak

SEKUENTZIA DIDAKTIKOAK: HASTEKO, 3 GALDERA

Zertarako balioko dizu gida honek?

IKTak ikasgelan aplikatzeko proposamen zehatz bat (sekuentzia didaktikoa) planifikatzeko eta praktikan jartzeko, eta proposamen horren bitartez, hauek lantzeko: oinarrizko gaitasunak eta arlokoak, curriculum-edukiak eta gaitasun digitalak.

Zer aurkituko duzu?

Gune elkarreragilea eta multimedia bat. Bertan, hauek zehazten dira: ikasgelarako programazioa, atazak IKTen bitartez egiteko orientabide didaktikoak, deskargarako estekak eta tutorialak.

Zer egin dezakezu?

Proposamena irakaskuntzan zuzenean aplikatu, zure ikasgelako testuingurura moldatu, adibideetatik abiatuta jarduera berriak sortu eta zure esperientziak beste irakasle batzuekin partekatu.

SEKUENTZIA DIDAKTIKOAK: HASTEKO, 3 GALDERA

Zertarako balioko dizu gida honek?

IKTak ikasgelan aplikatzeko proposamen zehatz bat (sekuentzia didaktikoa) planifikatzeko eta praktikan jartzeko, eta proposamen horren bitartez, hauek lantzeko: oinarrizko gaitasunak eta arlokoak, eduki kurrikularrak eta gaitasun digitalak.

Zer aurkituko duzu?

Gune elkarreragile eta multimedia bat. Bertan, hauek zehazten dira: ikasgelarako programazioa, atazak IKTen bitartez egiteko orientabide didaktikoak, deskargarako estekak eta tutorialak.

Zer egin dezakezu?

Proposamena irakaskuntzan zuzenean aplikatu, zure ikasgelako testuingurura moldatu, adibideetatik abiatuta jarduera berriak sortu eta zure esperientziak beste irakasle batzuekin partekatu.

SEKUENTZIA DIDAKTIKOAK: 5 GAKO

 Material irekia, pertsonalizatzeko modukoa eta berrerabilgarria
Erabilpen anitzekoa
Bertsio bereiziak irakasleentzat eta ikasleentzat
ADEaren erabilera ikasgelan
Plataforma- eta aukera-aniztasuna
MATERIALAK

Oinarriak

Zer da sekuentzia didaktiko bat eta zer eskaintzen digu?

Sekuentzia didaktiko bat (SD) jarduera-segida ordenatu bat da, ikasleak curriculum-gaitasuak zein IKT gaitasunak bereganatu ditzan diseinatua. Elkarren artean lotutako jardueren segida da sekuentzia didaktikoetako atalik esanguratsuena, ikasle orok segida horri jarraitu beharko baitio ikasketa-prozesuan.

Funtzio eta ezaugarri ezberdinak dituzten jarduerak lantzeko aukera eskaintzen digu, modu integratuan. Edukia aurkeztea, ulertzea, erabiltzea edo praktikatzea prozesuaren ezinbesteko osagaiak dira, eta elkarri lotutako edukien multzo esanguratsu baten inguruan lan egiteko aukera ematen dute.

Chaval Brasilen argazki bat, Flickr webgunean, CC lizentziapean.

Sekuentzia Didaktiko bakoitza HOD (Hezteko Objektu Digital) bat edo gehiagoz osatuta dago, eta hauek eskaintzen ditu:

  • Sekuentziako edukien deskribapena, aurkezpen interaktibo, kontzeptu-mapa, testu eta podcast formatuan, curriculum-edukiak hala uzten badu.
  • Edukiaren inguruko hasierako arakatze-jarduera.
  • Edukiaren inguruko jarraipen-jarduera.
  • Edukiaren inguruko laburpen- eta ebaluazio-jarduera.
  • Edukiaren sakontze-jarduera, aukerarik balego.

Hainbat jarduera egin daitezke, proposatutako jarduera-segidari jarraituz, edo horietako batzuk aukeratu eta norberaren sekuentziara egokitu.


Jardueretan zehar sortutako planteamenduek garatu egin nahi dituzte Lehen Hezkuntzarako Oinarrizko Gaitasunak (hizkuntza-komunikaziorakoa, matematikarakoa, mundu fisikoaren ezagutza eta harekiko elkarrekintzarakoa, gizarte- eta hiritar-gaitasuna, ikasten ikastekoa, eta norberaren autonomia eta ekimenerakoa) eta IKT gaitasunak (Eskola 2.0 proposamenean txertatutako ikasleen IKT gaitasunen maparen arabera).


Jarduerak, orokorrean, 2.0 baliabide digitalen erabileran eta sareko lanean oinarritzen dira. Horrenbestez, egindako proposamenetan ikasleak animatuko dira hainbat sare sozialetan informazioa kudea eta argitara dezaten, lankidetzan ari daitezen, eta, eskuratutako informazioa baloratzean, jarrera kritikoa zein hausnarkorra gara dezaten. Aldi berean, gune birtualetan adostutako arauak ezagutzeko eta aintzat hartzeko aukera izango dute.

Oinarriak

Sekuentzia didaktikoen xedea eta egitura

Sekuentzia didaktikoen xedea da ikasleek curriculum-edukiak ikastea eta gaitasun digitalak eskuratzea, IKTak ikasgelan aplikatzeko proposamen batetik abiatuta.

Ikasleek sekuentziako edukietan aurrera egingo dute etapaz etapa. Banaka egingo dute, baina taldeka egiteko jarduerak proposatuko zaizkie. Etapa bakoitzean adierazi egingo zaie zer egin behar duten eta zer baliabide erabili behar dituzten. Sekuentziek ikasleei eskaintzen dizkiete:

  • Hiru jarduerako edo gehiagoko segida bat, curriculum-edukiei heltzeko, Lehen Hezkuntzako 5. mailako ikasleei zuzendutako aginduekin.
  • Fitxategi erantsiak, jarduerak, koebaluazioa edo autoebaluazioa egiteko.
  • Ikasleentzako tutorialak, erabiliko diren programei edo web 2.0 zerbitzuei buruzkoak.
  • Sekuentziako IKT baliabide guztiak biltzen dituen atal bat.

Landuko den edukiaren arabera, hauek eskainiko dituzte:

  • Jarduerak egiteko erabiliko diren webguneetako, animazioetako eta bideoetako estekak
  • Ebazteko jarduera elkarreragileak

Sekuentziako irakasleentzako gidaren helburu nagusia da irakasleei laguntzea proposatutako ikasketa-segida planifikatzen eta praktikan jartzen. Premisa horiek kontuan hartuta, gidek irakasleei eskaintzen dizkiete:

  • Proposamen didaktikoaren testuingurua.
  • Orientabide didaktikoak, ADEaren metodologia erabiliz sekuentzia didaktikoak lantzeko.
  • Proposatutako jardueren erantzunak.
  • Oinarrizko gaitasunak eta arloaren berariazko gaitasunak.
  • IKT gaitasunak (Lehen Hezkuntzako 5. mailako ikasleentzako “Eskola 2.0” proposamenean ezarritakoak).
  • Ikasketa-helburuak, edukiak eta ebakuazio-irizpideak.
  • Proposamenean erabiliko diren materialak eta IKT baliabideak.
  • Prestakuntza-eduki osagarriak, irakasleei sekuentzia didaktikoak garatzen laguntzeko (ADEa, web 2.0 tresnak eta e-learning plataformak).

Oinarriak

Ebaluazioa

Ebaluazioak, burututako sekuentzien emaitzak aztertzeko tresna ez ezik, ikasketa-prozesua erregulatzekoa ere izan behar du. Horregatik, sekuentzia didaktikoan txertatuta egon behar du, prozesuan landuko diren jardueren parte izan. Jarduera horiek hausnarketa egiteko aukera eman behar diote ikasleari, egiten ari denaz, izan dituen zailtasunez, egin dituen akatsez, behar duen laguntzaz, eta hobetzeko eta aurrera egiteko bideez.

Ebaluazio hori hausnarketa-ariketa da, aurretiko ezagutzak prozesuan ikasten ari denarekin lotzeko aukera ematen duena. Akatsak abiapuntu gisa hartzen ditu, zailtasunez jabetzeko eta haiei aurre egiteko. Helburua ez da ikasleek zer ez dakiten jasotzea, jakitea baizik ezaguerak nola aplikatzen dituzten, informazioa nola lotzen duten, konponbideak bilatzeko trebetasunak nola aktibatzen dituzten... Ebaluazio horrek irizpide, adierazle eta ikasketa-helburu zehatzen multzo zabal bat izan behar du oinarrian, ez zenbakizko kalifikazio soil bat.

Gaitasunetan oinarritutako ebaluazioak lehenetsi egiten ditu ulertzea, aztertzea, lantzea, justifikatzea eta erantzunak argudiatzea, eta ez informazioa buruz ikastea eta errepikatzea.

Proposatutako jarduerak nahiz azterketa-, koebaluazio- eta autoebaluazio-tresnak irakasleen erreferenteak dira, ikasleen ikasketa-prozesua nahiz haiek lortutako emaitzak baloratzeko.

Oinarriak

Materialaren aurkezpena eta deskarga

Proiektu honen filosofiaren gakoetako bati jarraiki (arakatu, sortu, argitaratu eta partekatu), material hau irekia, pertsonalizatzeko modukoa eta berrerabilgarria da. Materiala erabiltzeko, ondorengo prozesuari jarraitu behar zaio. Gida egiteko erabili diren irudiak sekuentzia jakin bati dagozkio (Laburpena) eta, beraz, orientagarriak dira.

Sekuentzia didaktiko bakoitzak, ZIP fitxategi bat deskargatzeko atal bat dauka. Deskargatzeko materiala.

Lotura hori aukeratzean, ZIP fitxategi konprimatu bat deskargatzen da:

Gorde fitxategia botoian klik egingo dugu fitxategia gure ordenagailuan deskargatzeko. Behin ordenagailuan izanda, bi klik egingo ditugu fitxategiaren gainean, deskonprimatzeko programarekin ireki eta edukia ikusteko:

Landuko dugun materiala non gorde zehaztuko dugu eta karpetak bertara aterako ditugu.

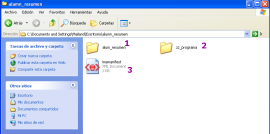
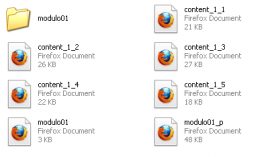
Behin materiala deskonprimatuta, karpeta zabaldu eta hiru karpeta ikusiko ditugu:

  1. Sekuentziaren edukia: Ikasl_sekuentzia

  2. Estiloarekin ikusteko behar diren artxiboak: Zz_programa

  3. Imsmanifest.xml fitxategi bat, Moodle-k edo antzeko plataforma batek prozesatzeko informazioa duena. Bertan, ikastaroaren edukiak zuzen azalduko zaizkio erabiltzaileari, dagokien balio pedagogikoa erantsita.

Oinarriak

Zer dago karpeta bakoitzean eta zertarako balio du?


Orain karpeta guztiak aztertuko ditugu.

Ikasl_sekuentzia

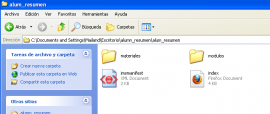
Sekuentzia guztiek dute Ikasl_sekuentzia izeneko karpeta bat.

  • Sekuentzia ikusteko lehen urratsa “index” fitxategia zabaltzea da eta sekuentzia guztian zehar nabigatzea.
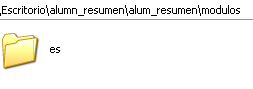
  • Moduluen karpetan hizkuntza direktorio bat dago. Guk “eu” karpeta ikusiko dugu, bertan baitago euskarazko bertsioa.

  • Karpeta barruan sekuentziaren .html fitxategi guztiak daude zenbakiz ordenatuta. Edozein eduki argitaratu nahi badugu, Dreamweaver (software jabeduna) edo Kompozer (software librea) erabil dezakegu.

  • “01modulua_p.html” fitxategia inprimatzeko bertsioari dagokio.
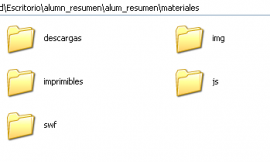
  • Materialen karpetan “img” karpeta nabarmentzen da, bertan baitaude sekuentziako irudi guztiak. Baten bat gehitu nahi bada, nahikoa da karpetan txertatzea eta dagokion html lotura egitea.
  • Modu berean, materiala ere txerta daiteke deskargen (fitxategi konprimatuak), .swf fitxategien (eskuliburu eta animazioak) eta inprimatzekoen karpetetan; bertan, materialaren .odt bertsioa dago, editatu eta .pdf formatura esportatu ahal izateko.

Zz_programa karpeta

Ondoren zz_programa karpetan sartuko gara, bertan baitaude sekuentzia ohiko estiloan bistaratzeko behar diren fitxategi guztiak.

Karpeta hori egituratik kanpo mugitzen badugu, materiala modu honetan ikusiko dugu:

Imsmanifest

“js” karpetak eta imsmanifest.xml fitxategiak ikasketarako plataforma birtualetako nabigatzaileei dagozkie, eta, beraz, ez da komeni haiek editatzea.

Helburu hauek hartu dira kontuan materialen egitura zehazteko:

  • Sekuentzian lantzen diren edukiak pertsonalizatzea.
  • Proposameneko edozein osagai gehitu, aldatu edo ezabatzeko aukera izatea.
  • Irudiak, materialak eta sekuentzien edukiak berrerabiltzeko aukera izatea.

Laguntza

Laguntza
  1. Ezker menua (goitik beherako ordena): sekuentziaren orri nagusiaren ikurra (home), iturriaren tamainaren ikurra, inpresio ikurra, laguntzarako sarrera ikurra eta edukinaren aurkibidearen ikurra.
  2. Materialaren izena barra eta sekzio aktualaren izenburua.
  3. Nabigazio geziak (hurrengo edo aurreko orrialdea).
  4. Edukinarentzako hutsunea.

Autor:

Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.

1. Material irekia, pertsonalizagarria eta berrerabilgarria

Sekuentzia didaktiko bakoitzak konprimatutako fitxategi bat dauka, deskargatzeko ZIP fitxategi bat, helburu hauekin:

  • Sekuentzian lantzen diren edukiak pertsonalizatzea
  • Proposamenean edozein atal gehitzea, aldatzea edo ezabatzea
  • Sekuentzietako irudiak, materialak eta baliabideak berrerabiltzea

Gonbidatzen zaitugu sekuentzia honen fitxategia deskargatzera eta askatasun osoz aztertzera. Esteka honetatik egin dezakezu.

Materialen egiturari edo sarbideari buruz laguntza edo orientabideak behar badituzu, ez utzi materialen erabilerari buruzko atala irakurri gabe.

2. Erabilpen anitzekoa

Sekuentzia didaktiko guztiak bi modutan erabil daitezke:

    • ONLINE: Kontsultak sarearen bidez eginez, prestakuntza-plataforma baten bitartez edota esteka edo URL baten bidez.
    • OFFLINE: ZIP fitxategi bat deskonprimatuz, ordenagailuan bertan lan egiteko, Internetera konektatu gabe.

3. Bertsio bereiziak irakasleentzat eta ikasleentzat

Sekuentzia didaktikoak sortzean, arreta berezia jarri da bi erabiltzaile-profiletan:

  • Irakasleek eskura dituzte ikasleei zuzenduriko lan-proposamena aztertzeko sarbidea, gida didaktikoa eta proposaturiko ariketen erantzunak.
  • Ikasleek eskura dituzte ariketen proposamena ikusteko sarbidea, eta proposamena praktikan jartzeko erabiliko dituzten materialen eta baliabideen zerrenda.

4. ADEaren erabilera ikasgelan

Sekuentzia didaktikoen diseinuak arbel digital elkarreragilea (ADE) erabiltzea sustatzen du. Horrela, irakasle batek ikasgelan hauek egin ditzake:

  1. Sekuentzia bat aztertu eta, bertatik, taldean aurkezteko edukiak hartu.
  2. Landu nahi dituen sekuentziaren edukiak, aurkezpenak, animazioak eta materialak proiektatu.
  3. Pixkanaka, praktika berritzaileak ikasgelako eguneroko lanean txertatu.
  4. Ariketa elkarreragileak, problemetako egoeren azterketak, eztabaidak eta taldeko zuzenketak erraztu.
  5. Arbelaren zentzua eta aurkeztutako edukiak indartzeko tresna eta funtzionalitate malguak erabili, ikasleen arreta lortzeko.

5. Plataforma- eta aukera-aniztasuna

Plataforma- eta aukera-aniztasuna

Sekuentzia didaktiko guztiak linean landu daitezke, besteak beste, Moodle edo LAMS plataformen bitartez, ikasleen jarraipenerako eta kontrolerako tresnak baliatuz. Sekuentziak Moodle-n erabili nahi baditugu, beharrezkoa izango da sekuentzien ZIP fitxategia deskargatzea (ikasleen bertsioa) eta Moodle, Blackboard edo antzeko ezaugarriak dituen plataforma batera inportatzea.

Horretarako, administratzaile-baimena behar da delako plataforma horietan, eta sistemak adieraziko dituen urratsak jarraitu (garrantzitsua da edukia nola inportatu azaltzen duen plataformako tutoriala oinarri hartzea).