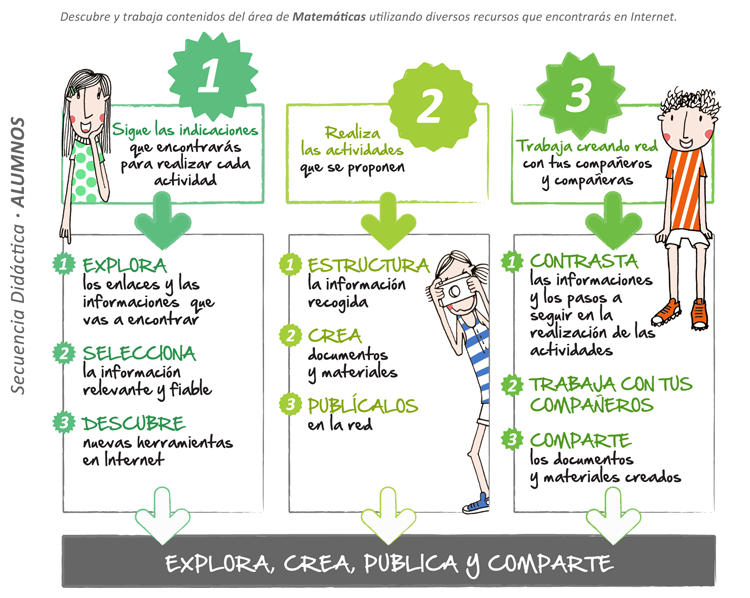
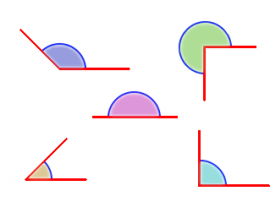
- Ángulos

- Guía para el profesorado

DIRECCIÓN: Narcís Vives
COLABORADORES:
- PRODUCCIÓN EJECUTIVA: Antonio Cara
- DIRECCIÓN CONTENIDOS: Mª Cristina Pérez y Magdalena Garzón
- DIRECCIÓN TÉCNICA: Maite Vílchez
- COORDINACIÓN ÁREA MATEMÁTICAS: José Orenga
- AUTORÍA: Eider Antxustegi-Etxarte
- CORRECCIÓN ESTILO VERSIÓN CASTELLANA: Anna Betriu y Joan Martín
- ADAPTACIÓN EUSKERA: Bakun itzulpen eta argitalpen zerbitzuak, s.l.
- MAQUETACIÓN: Maite Vílchez y Miquel Gordillo
Ayuda

- Menú izquierdo (en orden de arriba a abajo): icono página principal del curso (home), icono tamaño de la fuente, icono impresión del módulo, icono acceso a la ayuda e icono índice del contenido.
- Barra nombre del material y título de la sección actual.
- Flechas de navegación (página siguiente o anterior).
- Espacio para el contenido.
Autor:
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Copyright:
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Recursos
Estos son los recursos TIC que utilizarás para trabajar a lo largo de esta secuencia didáctica:
Referencias web |
http://www.genmagic.org/mates1/ra1c.swf Descripción: introducción a los conceptos de recta y ángulo y sus tipos
http://www.euskalnet.net/jesusgo Descripción: transportador de ángulos virtual
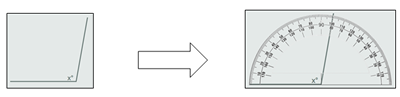
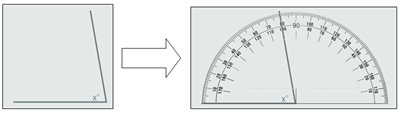
http://www.educaplus.org/play-10-Transportador.html Descripción: medida de ángulos con transportador virtual
http://www.educaplus.org/play-162-Estimaci%C3%B3n-de-%C3%A1ngulos.html Descripción: estimación de la medida de un ángulo
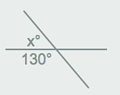
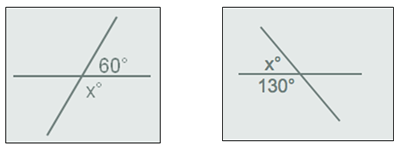
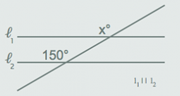
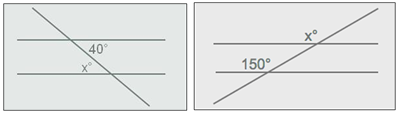
http://www.thatquiz.org/es/practicetest?iw23rmnz46cu Descripción: ángulos formados por rectas que se cortan
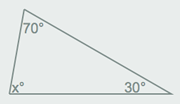
http://www.thatquiz.org/es/practicetest?iy243msw48f8 Cálculo del valor de ángulos de triángulos, con o sin transportador
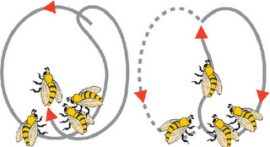
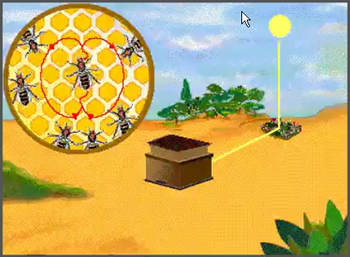
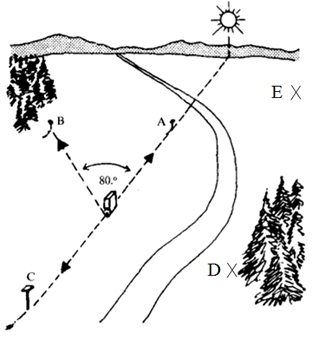
http://www.youtube.com/watch?v=-7ijI-g4jHg Baile de las abejas en la colmena
http://www.solociencia.com/biologia/05062301.htm Información reciente (septiembre de 2010) sobre las últimas investigaciones realizad as en el tema del baile de las abejas.
Descripción de una ruta por la isla
Ruta de Indautxu, San Mamés y Museo de Bellas Artes
Ruta de Guggenheim, Ayuntamiento y Teatro Arriaga |
Un poco de historia
La geometría tras Euclides y los tres problemas de la Antigüedad
Euclides fue el gran sistematizador de todas las matemáticas anteriores a él. No sólo recopiló todo
el saber matemático previo, sino que estableció las bases para la construcción de cualquier teoría matemática, aceptando
que se puede partir de axiomas o postulados (proposiciones intuitivamente claras y evidentes, que no requieren demostración)
y sobre ellos construir un razonamiento axiomático-deductivo (demostrando cada paso) que nos permita llegar a conclusiones
fiables. Su sistema se sintetiza en su obra cumbre, Los elementos, en la que partiendo de sólo cinco postulados y
algunas definiciones construye toda la geometría y la aritmética conocidas hasta el momento. Su obra marcará el conocimiento
geométrico hasta entrado el siglo XIX. |
Fragmento de uno de los Papiros de Oxirrinco,
con unas líneas de Los elementos de Euclides. |
Después de Euclides
Euclides finaliza el edificio de la Geometría griega y tras él solamente dos personajes desarrollan teorías relacionadas con las figuras curvas: Arquímedes y Apolonio.
Arquímedes estudió ampliamente las secciones cónicas, introduciendo en la geometría las primeras
curvas que no eran ni rectas ni circunferencias. Además, realizó el cálculo del volumen de la esfera basándose en los del
cono y el cilindro.
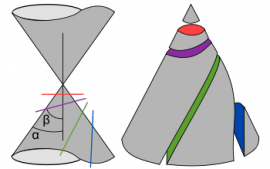
Las secciones cónicas son aquellas que resultan de cortar un cono y un plano. Según la posición del plano aparecen: circunferencias,
elipses (recordad que la órbita de la Tierra alrededor del Sol es una elipse), parábolas (recordad que el movimiento que describe
una bala de cañón es una parábola) e hipérbolas.
Apolonio trabajó en varias construcciones de tangencias entre círculos, así como en secciones cónicas y otras curvas. Su nombre ha quedado ligado al Cono de Apolonio, una figura, normalmente de madera, que se puede separar en trozos según los cortes con los planos y entonces se ven las cuatro cónicas que se obtienen.
Cono de Apolonio
Fuente: http://matematica3eduintegral05lg.espacioblog.com/post/2008/10/27/geometria
Los tres problemas de la Antigüedad
La Geometría griega plantea tres problemas para resolver con regla y compás que se conocen como los Tres problemas de la Antigüedad. No se consiguieron resolver ninguno de los tres.
- La duplicación del cubo
Cuenta la leyenda que para combatir una peste que asolaba Atenas se envió a un grupo de sabios al
Oráculo de Delfos, consagrado a Apolo, para descubrir qué se debía hacer para conseguir que la enfermedad remitiera.
La respuesta fue que se debía duplicar el altar consagrado a Apolo en la isla de Delos. El altar era peculiar: era
de forma cúbica. Los atenienses construyeron un altar cúbico cuyos lados eran el doble de las del altar de Delos,
pero la peste no cesó, se volvió más mortífera. Consultado nuevamente, el oráculo advirtió a los atenienses que el
altar no era el doble de grande, sino 8 veces mayor, puesto que el volumen del cubo es el cubo de su lado ((2 x lado)3
= 23 x lado 3 = 8 x lado 3). Nadie supo cómo construir un cubo cuyo volumen
fuese exactamente el doble del volumen de otro cubo dado y el problema matemático persistió durante siglos. |

Delos, lugar del nacimiento de Apolo |
- La cuadratura del círculo
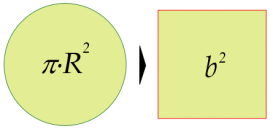
El problema de la cuadratura del círculo consiste en, dado un círculo, obtener un cuadrado cuyo área mida exactamente lo mismo que el área del círculo. Anaxágoras fue el primero en intentar resolverlo (sin éxito), dibujando en las paredes de su celda cuando fue hecho prisionero por explicar desde la lógica diversos fenómenos que los griegos atribuían a los dioses. Tampoco pudo ser resuelto por los geómetras de la Antigüedad y se añadió a los dos problemas anteriores extendiéndose que su resolución era imposible. En 1882, el matemático alemán Ferdinand Lindemann probó que, debido a las características especiales del número π que aparece en el área del círculo, no es posible cuadrar el círculo usando regla y compás, con lo que el problema quedó como de resolución imposible. |
|
- La trisección del ángulo

Este problema consiste en dividir un ángulo cualquiera en tres ángulos iguales, empleando únicamente la regla y el compás. Aunque aparentemente es sencillo (es muy fácil dividir el ángulo en dos partes o en cuatro) no lo es en realidad y tampoco lograron resolver este reto.
Fuente imagen: http://www.portalplanetasedna.com.ar/problemas_griegos02.htm

Ángulos
Haz clic en la imagen para avanzar: