1. jarduera

Angeluak. Definizioa eta sailkapena

Angelu esaten zaio jatorri bereko bi zuzenerdik mugatutako planoaren zatiari.

Angelua osatzen duten zuzenerdiak angeluaren aldeak dira, eta elkartzen diren puntua, erpina.

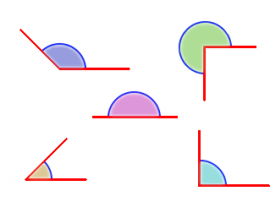
Angeluen sailkapena:

• Angelu laua: (180º) planoaren erdia hartzen du, eta angeluaren erpinean jatorria duten aurkako bi zuzenerdik osatzen dute.
• Angelu zuzena: (90º) angelu lauaren erdia da, eta bi zuzenerdi elkarzutek osatzen dute.
• Angelu zorrotza: (<90º) angelu zuzena baino txikiagoa.
• Angelu kamutsa: (>90º) angelu zuzena baino handiagoa eta laua baino txikiagoa.

Bestalde, modu orokor batean sailka ditzakegu angeluak, ahurretan eta ganbiletan:

• Angelu ahurra: (>180º) angelu laua baino handiagoa.
• Angelu ganbila: (<180º) angelu laua baino txikiagoa.

Esteka honetan azalpen bat aurkituko duzue, zuzenei eta angeluei lotuta, beharko dituzuen alderdi teorikoei buruz —hautatu hirugarren aukera: angeluak—.

Jarduerak

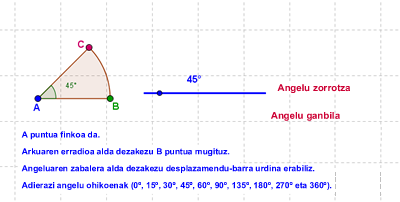
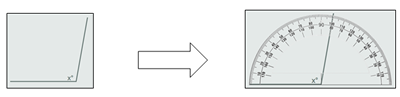
Angeluak marraztuko ditugu tresna elkarreragile baten bidez. Tresna horrek uneoro adieraziko digu zenbatekoa den zuzenkien arteko angelua. Honelako irudi bat erakutsiko digu aplikazioak:

Tresna hori erabiliz, zirkunferentziaren neurri desberdineko angeluak marraz ditzakezue, zer motatakoak diren egiaztatu (zorrotzak, ganbilak, kamutsak...), eta haien zabalera gradutan jakin.

Aplikazioan angelu ohikoenak marrazteko proposatzen da, hurrengo mailetan agertuko baitira, trigonometria ikastean.

Egin klik hemen aplikazioa abiarazteko.

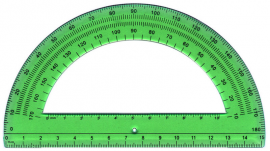
Goniometroa eta angelu-garraiagailua erabiltzen da angeluak neurtzeko. Egin klik hemen zenbait jarduera egiteko, tresna horren erabilerari lotuta. Mugitu garraiagailua angeluaren gainean, eta idatzi azpian neurtutako balioa.

Jarduera honetan, angeluak identifikatu behar dituzue, eta zer motatakoak diren esan. Horrez gain, angeluaren balioa kalkulatu behar duzue, gradu hirurogeitarretan. Hemen duzue adibide bat, ariketen orrian ageri diren angeluekin zer egin behar duzuen jakiteko:

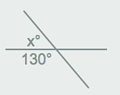
Ezkerreko angelua, esaterako, kamutsa eta ganbila da, eta 150º-ko zabalera du.

Osatu dokumentu honetako taula.

Laguntze aldera, dokumentua inprima dezakezue, eta angelu-garraiagailua erabili.

Egin klik hemen erantzunak ikusteko.

Jarraian, zenbait egoeratan aurki ditzakegun angelu batzuen zabalerak kalkulatuko ditugu. Ekin aurretik, jolas hauek erabil ditzakezue, angeluen kalkulua praktikatzeko:

• Kalkulatu angeluen zabalera angelu-garraiagailuaz hemen.

• Jolastu angeluen gutxi gorabeherako zabalera asmatzen hemen.

Orain, egoera horiei helduko diegu:

1.

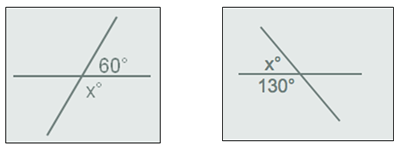
Elkar ebakitzen duten bi zuzenen arteko angeluaren zabalera dakigunean, kontuan hartu angeluak osagarriak direla, hau da, bien batura 180º dela. Beraz, adibide honetan, xº = 180º – 130º = 50º.

• Egin klik hemen erantzuna egiaztatzeko (ezkerreko jarduera).

Kalkulatu xº adibide hauetan:

2.

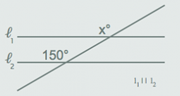
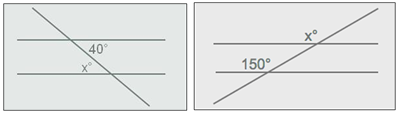
Bi zuzen paralelo ebakitzen dituen beste zuzen bat izanda, angeluetako baten zabalera dakigunean, kontuan hartu beste zuzen paraleloarekin osatzen duena balio berekoa dela. Beraz, adibide honetan, xº = 150º.

• Egin klik hemen erantzuna egiaztatzeko (eskuineko jarduera).

Kalkulatu xº adibide hauetan:

3.

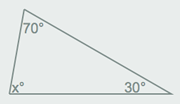
Triangelu baten bi angeluren balioak jakinda hirugarrena kalkulatu behar badugu, kontuan hartu hiru angeluen batura 180º dela beti. Beraz, adibide honetan, xº = 180º – ( 70º + 30º ) = 80º

• Egin klik hemen erantzuna egiaztatzeko.

Kalkulatu xº adibide hauetan:

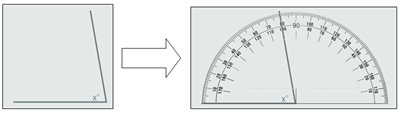
• Neurtu angeluaren zabalera zuzenean angelu-garraiagailua erabiliz. Kokatu goniometroaren zirkunferentziaren zentroa angeluaren erpinaren gainean, eta oinarriaren aldeetako bat, angeluaren aldeetako baten gainean:

Kalkulatu angelu honen zabalera angelu-garraiagailua adierazi bezala erabiliz:

Irudia: Luigi Chiesa, Wikipedia