ZUZENDARITZA: Narcís Vives
KOLABORATZAILEAK:
- PRODUKZIO-ZUZENDARITZA: Antonio Cara
- EDUKI-ZUZENDARITZA: Mª Cristina Pérez eta Magdalena Garzón
- ZUZENDARITZA TEKNIKOA: Maite Vílchez.
- MATEMATIKA ARLOAREN KOORDINAZIOA: José Orenga
- EGILEA: Eider Antxustegi-Etxarte
- GAZTELERAZKO BERTSIOAREN ESTILO-ZUZENKETA: Anna Betriu eta Joan Martín
- EUSKARARA ITZULPENA: Bakun itzulpen eta argitalpen zerbitzuak, s.l.
- MAKETAZIOA: Maite Vílchez eta Miquel Gordillo
Laguntza
- Ezker menua (goitik beherako ordena): sekuentziaren orri nagusiaren ikurra (home), iturriaren tamainaren ikurra, inpresio ikurra, laguntzarako sarrera ikurra eta edukinaren aurkibidearen ikurra.
- Materialaren izena barra eta sekzio aktualaren izenburua.
- Nabigazio geziak (hurrengo edo aurreko orrialdea).
- Edukinarentzako hutsunea.
Autor:
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Copyright:
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Baliabideak
Hauek dira sekuentzia didaktiko honetan erabiliko dituzuen IKT baliabideak:
Web-erreferentziak |
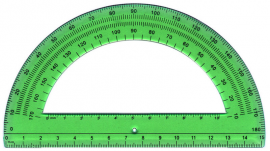
http://www.genmagic.org/mates1/ra1c.swf Deskribapena: zuzenak eta angeluak zer diren eta zer motatakoak izan daitezkeen.
http://www.euskalnet.net/jesusgo Deskribapena: angelu-garraiagailu birtuala.
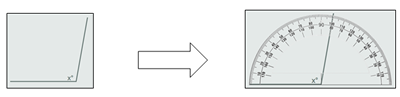
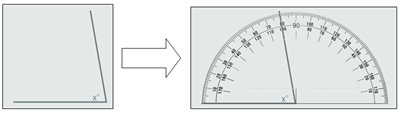
http://www.educaplus.org/play-10-Transportador.html Deskribapena: angeluen neurketa garraiagailu birtual bidez.
http://www.educaplus.org/play-162-Estimaci%C3%B3n-de-%C3%A1ngulos.html Deskribapena: angeluen zabaleren iritzirako kalkulua.
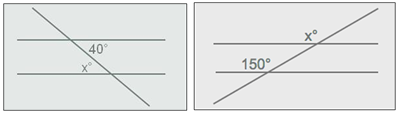
http://www.thatquiz.org/es/practicetest?iw23rmnz46cu Deskribapena: elkar mozten duten zuzenen arteko angeluak.
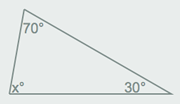
http://www.thatquiz.org/es/practicetest?iy243msw48f8 Deskribapena: triangeluen angeluen zabaleren kalkulua, garraiagailua erabiliz nahiz erabili gabe.
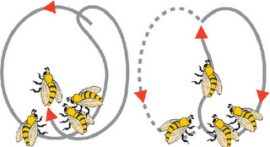
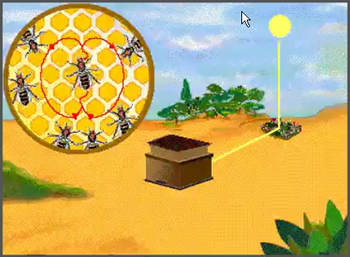
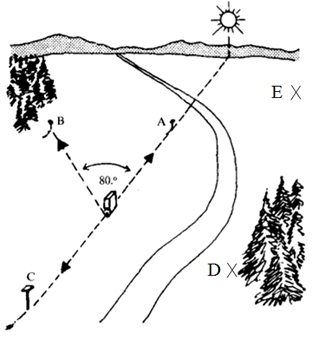
http://www.youtube.com/watch?v=-7ijI-g4jHg Deskribapena: erleen dantza erlauntzan.
http://www.solociencia.com/biologia/05062301.htm Deskribapena: 2010eko iraileko informazioa, erleen dantzari buruz egindako azken ikerketei buruz.
Uhartean zehar ibilbide baten deskribapena.
Indautxu, San Mames eta Arte Ederren Museoa lotzen dituen ibilbidea.
Guggenheim Museoa, udaletxea eta Arriaga Antzokia lotzen dituen ibilbidea. |
Historia apur bat
Geometria Euklidesen ondoren eta Antzinaroko hiru problemak
Euklides izan zen bere aurreko matematika-ezagutza guztien sistematizatzaile handia. Bere aurreko
matematika-jakintza guztia biltzeaz gain, matematika-teoria oro osatzeko oinarriak ezarri zituen. Horretarako, axiometatik
edo postulatuetatik abia gaitezkeela onartuta —alegia, frogaketa beharrik ez duten intuiziozko proposizio argi eta bistakoetatik—,
dedukziozko arrazoiketa axiomatiko bat osatu behar dela esan zuen, ondorio fidagarriak lortzea ahalbidetuko duena. Elementuak
da Euklidesen lan nagusia, eta haren sistema laburbiltzen du. Bertan, ordura arteko geometria eta aritmetika azaltzen ditu,
bost postulatutatik eta definizio batzuetatik abiatuta. Haren lanak markatu zuen geometria-ezaguera XIX. mendera arte. |
Oxirrinko-ko papiroetako bat, Euklidesen Elementuak lanaren lerro batzuk jasotzen dituena. |
Euklidesen ondoren
Euklidesek osatu zuen Greziako geometria-ezaguera. Haren ondoren, bi pertsonaiak soilik garatu zituzten irudi makurrekin lotutako teoriak: Arkimedesek eta Apoloniok.
Arkimedesek sakon aztertu zituen sekzio konikoak. Hori horrela eginda, lehen kurbak txertatu zituen
matematikan —zuzenak edo zirkunferentziak ez ziren lehen lerroak—. Horrez gain, esferaren bolumena kalkulatu zuen, konoaren
eta zilindroaren bolumenak oinarri hartuta.
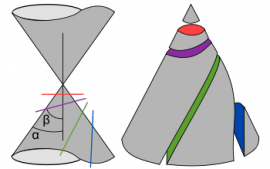
Sekzio konikoak dira kono bat plano batez ebakitzean eratzen direnak. Planoaren posizioaren arabera, zenbait motatakoak izan
daitezke: zirkunferentziak, elipseak —gogoratu Lurraren orbita Eguzkiaren inguruan elipse bat dela—, parabolak —esaterako,
kanoi batek jaurtitako balak egiten duen ibilbidea— eta hiperbolak.
Apoloniok zirkuluen ukitzea, sekzio konikoak eta beste kurba batzuk aztertu zituen. Bere izena daraman konoari lotuta gogoratzen dugu. Apolonioren konoa zurezko gorputz bat da, lau ebaketa dituena planoaren balizko lau posizioen arabera. Zatiak askatu egin daitezke sekzio konikoen lau motak ikusteko.
Apolonioren konoa.
Iturria: http://matematica3eduintegral05lg.espacioblog.com/post/2008/10/27/geometria
Antzinaroko hiru problemak
Greziako geometriak hiru problema proposatu zituen, erregela eta konpasa erabiliz ebazteko. Antzinaroko hiru problemak esaten zaie, eta ez da lortu bakar bat ere ebazterik.
- Kuboaren bikoizketa
Elezahar batek dioenez, atenastarrek jakintsu talde bat bidali zuten Delfoseko orakuluarengana haiek
hiltzen ari zen izurri latzari irtenbide bat bilatzeko. Orakuluak Delosen Apolori eskainitako aldarea bikoiztu behar zutela
erantzun zien. Aldaren bereizgarria zen kubo forma. Atenastarrek aldare berri bat eraiki zuten aldeak Delosekoarenak halako
bi zituena; baina izurriaren eragina ez zen gutxitu, aitzitik, hilgarriago egin zen. Horrela, berriro joan ziren orakuluarengana
erantzun eske. Orakuluak adierazi zien aldare berria ez zela aurrekoaren bikoitza, zortzi aldiz handiagoa baizik. Izan ere
kuboaren bolumena kalkulatzeko aldearen luzera ber hiru egin behar da ((2 x aldea)3 = 23 x
aldea 3 = 8 x aldea 3). Inork ez zuen asmatu nola eraiki kubo bat bolumena emandako
batena halako bi zuena. Problema hark ebatzi gabe iraun zuen mendeetan. |

Delos, Apoloren jaiolekua. |
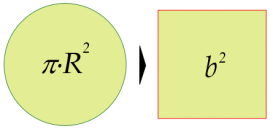
- Zirkuluaren koadratura
Zirkuluaren koadratura esaten zaio zirkulu bat emanda haren azalera berdina duen karratu bat lortzeari. Anaxagoras izan zen problema hura ebazten saiatzen lehena, baina ez zuen lortu. Anaxagoras bere zigor-gelako hormetan marrazkiak eginez saiatu zen problema hura ebazten, izan ere, preso hartu zuten ustez jainkotiarrak ziren gertaera batzuk logikaren ikuspegitik azaldu zituenean. Antzinaroko geometrek ere ez zuten lortu problema hura ebazterik, eta ebazpena ezinezkotzat jo zen. 1882an Ferdinand Lindemann alemaniar matematikariak frogatu zuen ezinezkoa dela erregela eta konpasa erabiliz zirkuluaren koadratura lortzea, zirkuluaren azaleran ageri den π zenbakiaren ezaugarri bereziak direla eta. Horrela egiaztatu zen problema ebatzi ezina zela. |
|
- Angeluen trisekzioa

Problema horren xedea da angelu bat zabalera berdineko hiru angelutan banatzea, erregela eta konpasa soilik erabiliz. Itxuraz erraza den arren —oso erraza da angeluak bitan edo lautan banatzea—, ez da hala, eta ez zuten lortu erronka hori gainditzerik.
Iturria: http://www.portalplanetasedna.com.ar/problemas_griegos02.htm

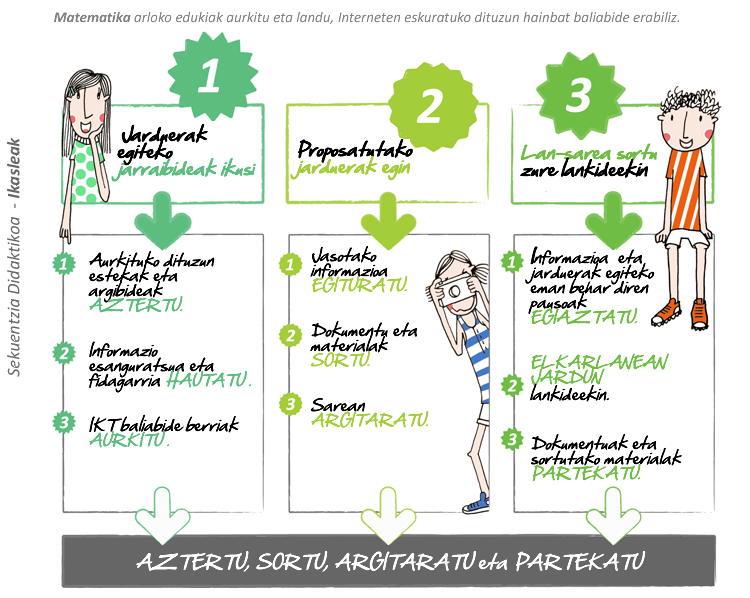
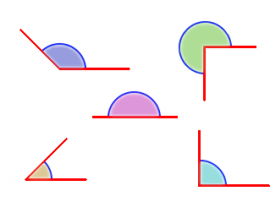
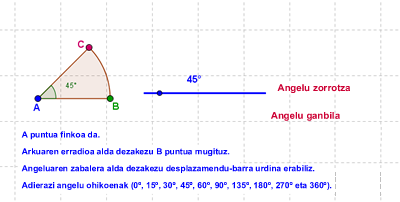
Angeluak
Egin klik irudian, aurrera egiteko: