- Iraupena:
- ordubete
- Taldekatzea:
- taldean
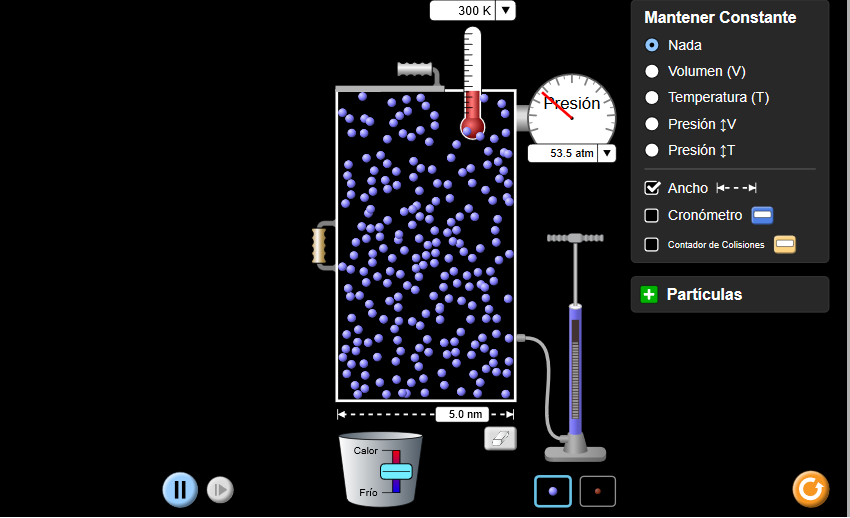
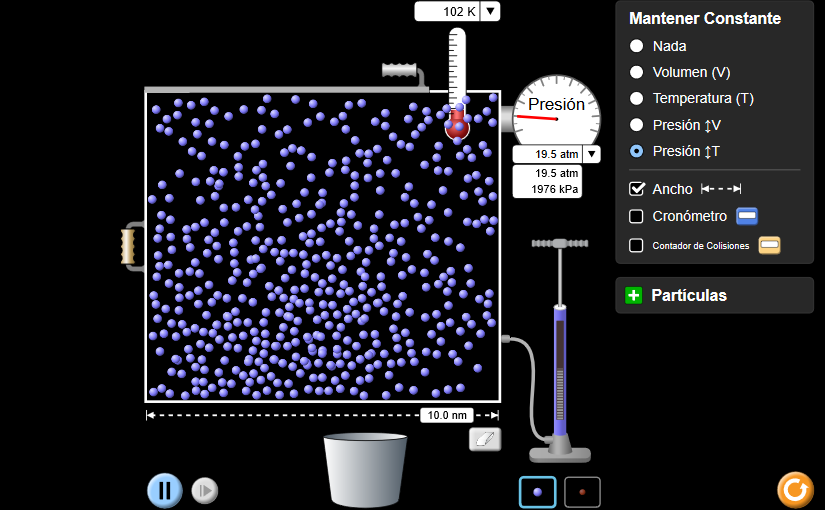
3. Gasen legeak laburbiltzeko eta ondorioak ateratzeko
Taula hau beteko dugu:
| Erlazioa |
Zuzena ala alderantzizkoa? |
Parametro konstanteak |
Norena da legea? |
Arrazoia labur azaldu, partikulen ereduaren arabera. |
| V vs P |
|
|
|
|
| V vs T |
|
|
|
|
| T vs P |
|
|
|
|
4. Agertokiak
Gasen legeak baliatuz, hurrengo agertoki hauek azalduko ditugu. Kasu bakoitzean, erantzunerako ebidentzia gisa zein grafiko erabil daitekeen aipatuko dugu.
- Zergatik dirudite bizikletako pneumatikoek lauagoak neguan udan baino?
- Zergatik lehertzen da freskagarri lata bat eguzkitan uzten bada?
- Gasez betetako ontzi zurrun bat izotzetan jartzen da (adibidez: esprai botila bat). Zer gertatuko da gasaren presioarekin? Zer gertatuko da bolumenarekin?
- Infektatutako hortz batek gasez bete den abzesua sortu du (infektatutako ehun-eremua). Abzesuak presioa egiten du hortzaren nerbioan, eta haginetako mina eragiten du. Dentistarenera joan bitartean, haginetako mina zuen pertsona mina arintzen saiatu zen, infektatutako eremua bero hezearekin tratatuz. Lagunduko ote dio tratamendu horrek? Zergatik edo zergatik ez?
5. Orokortuz: Gas idealen legeak
Boyle-Mariotte, Charles eta Gay-Lussacen legeak betetzen dituzten gasei gas perfektuak edo idealak deitzen zaie. Gasen legeak ekuazio sinple bakarrean konbina daitezke, tenperatura eskala absolutuan edo Kelvinetan adierazten bada. Honela, Charlesen legeak eta Gay-Lussacen legeak hau adierazten dute, hurrenez hurren:
V = k .T (1)
P= k .T (2)
Bestalde, Boyleren legeak ezartzen du V eta P alderantziz proportzionalak direla; alegia:
V= k (3)
Ekuazio hauek konbinatuz, P.V/T = K daukagu. Presioaren eta bolumenaren arteko biderkadura, zati tenperatura kelvin gradutan, konstante bat da; edo bestela esanda:
P1.V2/T1 = P2.V2/T2
Aplika dezagun lege orokortu hori bi egoeratan:
- 4 atmosferako presioan eta 11 ° C-ko tenperaturan dagoen urpekari baten oxigeno-depositutik 25 mL-ko burbuila bat askatu da. Zein da burbuilaren bolumena ozeanoaren azalera iristen denean, non presioa 1 atm-koa den eta tenperatura 18 ° C-koa?
- 750 mL-ko globo aerostatiko bat helioz puztu da 8 ° C-ko tenperaturan eta 380 atmosferako presioan. Zein da globoaren bolumen berria, atmosferan 0,20 atm-ko presioan eta – 45 ° C-ko tenperaturan